解决非线性问题的另种技术是添加相似特征。这些特征经过相似函数计算得出,相似函数可以测量每个实例与一个特定地标之间的相似度。以前面提到过的一维数据集为例,在x=-2和x=1处添加两个地标。接下来,我们采用高斯径向基函数(RBF) 作为相似函数,y=0.3
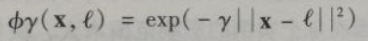
高斯RBF
这是一个从0 (离地标差得非常远)到1 (跟地标-样)变化的钟形函数。现在我们准备计算新特征。例如,我们看实例x1=-1:它与第一个地标的距离为1,与第二个地标的距离为2。因此它的新特征为x2=eps(-0.3 12)≈0.74, x3=eps(-0.322)≈0.30.下图的右图显示了转换后的数据集(去除了原始特征),现在你可以看出,数据呈线性可分离的了。
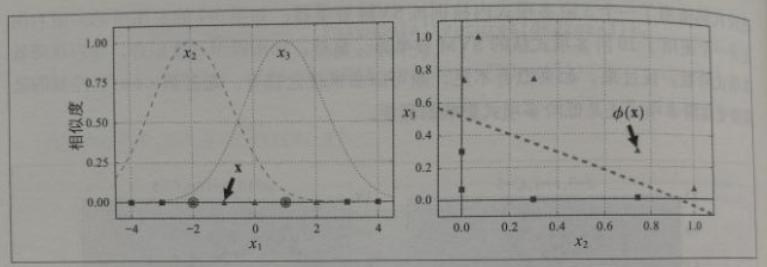
如何选择地标呢?最简单的方法是在数据集里每一个实例的位置上创建个地标。这会创造出许多维度,因而也增加了转换后的训练集线性可分离的机会。缺点是,一个有m个实例n个特征的训练集会被转换成一个m个实例m个特征的训练集,假设抛弃了原始特征。如果训练集非常大,那就会得到同样大数量的特征。


