哥尼斯堡(今俄罗斯加里宁格勒)是东普鲁士的首都,普莱格尔河横贯其中。十八世纪在这条河上建有七座桥,将河中间的两个岛和河岸联结起来。人们闲暇时经常在这上边散步,一天有人提出:能不能每座桥都只走一遍,最后又回到原来的位置。这个看起来很简单又很有趣的问题吸引了大家,很多人在尝试各种各样的走法,但谁也没有做到。看来要得到一个明确、理想的答案还不那么容易。
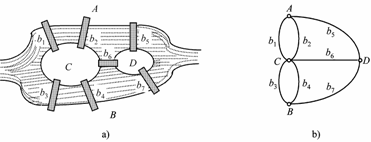
1736年,有人带着这个问题找到了当时的大数学家欧拉,欧拉经过一番思考,很快就用一种独特的方法给出了解答。欧拉把这个问题首先简化,他把两座小岛和河的两岸分别看作四个点,而把七座桥看作这四个点之间的连线。那么这个问题就简化成,能不能用一笔就把这个图形画出来。经过进一步的分析,欧拉得出结论——不可能每座桥都走一遍,最后回到原来的位置。并且给出了所有能够一笔画出来的图形所应具有的条件。


