马尔可夫决策过程简介
马尔可夫决策过程(Markov Decision Processes,MDP)是对强化学习中环境的形式化的描述,或者说是对于智能体所处的环境的一个建模。在强化学习中,几乎所有的问题都可以形式化地表示为一个马尔可夫决策过程。本文以Frozen Lake游戏为例,介绍一下马尔可夫决策过程。
Frozen Lake 游戏介绍
Frozen Lake游戏的场景是一个结了冰的湖面(即 4×4 大小的方格),要求从开始点“Start”走到目标点“Goal”,且不能掉进冰窟窿里。
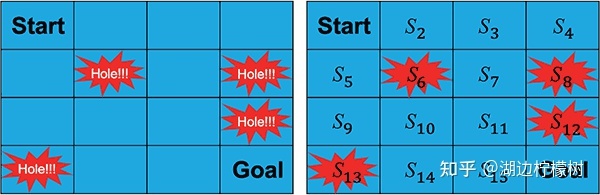
游戏有两种模式:“有风”模式和“无风”模式。两种模式的区别是,在“有风”模式下,智能体的移动会受到风的影响,例如,智能体当前的位置是 S3,智能体选择向右走一步,“无风”模式下智能体会到达 S4状态,而在“有风”模式下,智能体的位置就不确定了,有可能会被风吹到任意状态,例如 S7。
在Frozen Lake游戏中,智能体从“Start”走到目标点“Goal”需要经过一个序列的中间状态,同时也需要根据策略做出一系列的动作。通常根据智能体执行完一个序列的动作后所获得的累积奖励来评判这个策略的优劣,累积得到的奖励越大,则认为策略越优。
计算累积奖励有两种方式,一种是计算从当前状态到结束状态的所有奖励值之和:
Gt=rt+1+rt+2+...+rt+T
上面适用于有限时界(Finite-horizon)情况下的强化学习,但是在有些无限时界(Finite-horizon)情况,智能体要执行的可能是一个时间持续很长的任务,比如自动驾驶,如果使用上式计算累积奖励值显然是不合理的。
需要一个有限的值,通常会增加一个折扣因子,如下式:
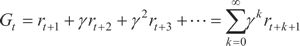
在上式中,0≤γ≤1 。当 γ 的值等于 0 时,则智能体只考虑下一步的回报;当 γ 的值越趋近于 1,未来的奖励就会被越多地考虑在内。需要注意的是,有时候我们会更关心眼下的奖励,有时候则会更关心未来的奖励,调整的方式就是修改 γ 的值。
什么是马尔可夫决策过程?
我们将马尔可夫决策过程定义为一个五元组:M=(S,A,R,P,γ)
S:状态空间,例如在Frozen Lake游戏中,总共有 16 个状态(Start,S2,…,S15,Goal);
A:动作空间,在Frozen Lake游戏中,每个状态下可以执行的动作有四个(上、下、左和右);
R:奖励函数,在某个状态 St 下执行了一个动作并转移到下一个状态 St+1,就会得到一个相应的奖励 rt+1;
P:状态转移规则,可以理解为我们之前介绍的状态转移概率矩阵。在某个状态 St 下执行了一个动作,就会以一定的概率转移到下一个状态 St+1。


