1、梯度下降法简介
梯度下降法(英语:Gradient descent)是一个一阶最优化算法,通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。
2、梯度下降法原理介绍

3、梯度下降法举例说明
梯度下降算法在机器学习与神经网络中有广泛的应用,主要用来求最优参数,本文通过一个最简单的例子来演示梯度下降算法过程
举例:y = x ^ 2 ,通过梯度下降算法求y取最小值(极小值)时候的最优解x,求解过程主要通过迭代完成
迭代的方程为:x = x - y'(x) * α
其中:
(1)x为要求的解,y'(x)为梯度(也就是导数或偏导,我们在这里用最简单的一元函数演示,所以直接写成导数)
(2)α为学习率(或称步长,是一个重要的参数,α的选择直接影响这着算法的效率)
算法过程如下所示:
1、首先任取一点,我们取x = 3,计算其导数y'(x) = 6
2、我们设定学习率为α = 0.4
3、开始算法的迭代:
(1)x = 3,y'(x) = 6,x = x - y'(x) * α = 0.6
(2)x = 0.6,y'(x) = 1.2,x = x - y'(x) * α = 0.12
(3)x = 0.12,y'(x) = 0.24,x = x - y'(x) * α = 0.024
(4)x = 0.024,y'(x) = 0.048,x = x - y'(x) * α = 0.0048
。。。
4、当梯度(导数)下降到很小或为0时,则求得的解x趋向最优解,比如本例中迭代到第四步时y'(x) = 0.048已经非常小了,x = 0.0048基本趋向于本例的真正解x = 0
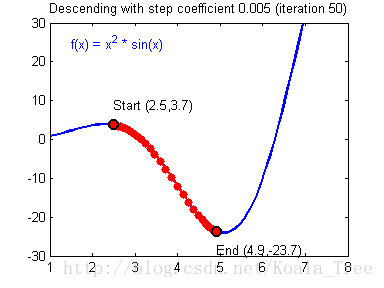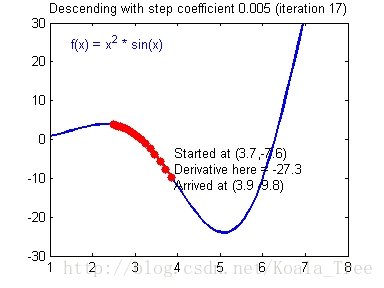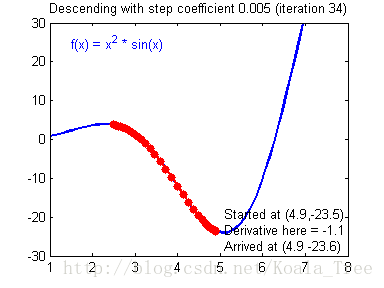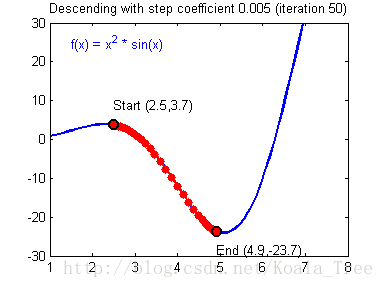
4、梯度下降法效果演示