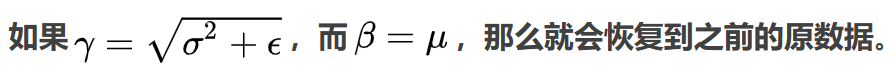1、Batch Normalization简介
Batch Normalization,简称BN,由Google于2015年提出,这是一个深度神经网络训练的技巧,它不仅可以加快了模型的收敛速度,并且在一定程度缓解了深层网络中“梯度弥散”的问题,从而使得训练深层网络模型更加容易和稳定,所以目前Batch Normalization已经成为几乎所有卷积神经网络的标配技巧。
在Batch Normalization出现之前,我们的归一化操作一般都在数据输入层,对输入的数据进行求均值以及求方差做归一化,但是Batch Normalization的出现打破了这一个规定,我们可以在网络中任意一层进行归一化处理,因为我们现在所用的优化方法大多都是min-batch SGD,所以我们的归一化操作就成为Batch Normalization。
2、Internal Covariate Shift问题
训练深度网络的时候经常发生无法收敛的问题,因为每一次参数迭代更新后,上一层网络的输出数据经过这一层网络计算后,数据的分布会发生变化,为下一层网络的学习带来困难,神经网络本来就是要学习数据的分布,要是分布一直在变,学习就很难了。这种现象被称为“Internal Covariate Shift”,Batch Normalization的提出,就是要解决在训练过程中中间层数据分布发生改变的问题。
3、Batch Normalization的设计思想
为了解决Internal Covariate Shift问题,我们可以直接对神经网络的每一层做归一化,假设将每一层输出后的数据都归一化到0均值,1方差,满足正太分布,但是,此时出现了一个新问题,每一层的数据分布都是标准正太分布,导致其完全学习不到输入数据的特征,因为费劲心思学习到的特征分布被归一化了,因此,直接对每一层做归一化显然是不合理的。但是如果稍作修改,加入可训练的参数做归一化,这就是Batch Normalization的设计思想,下图的伪代码可以看出来:

如上图所示,Batch Normalization步骤主要分为4步:
1、求每一个训练批次数据的均值
2、求每一个训练批次数据的方差
3、使用求得的均值和方差对该批次的训练数据做归一化。其中ε是为了避免除数为0时所使用的微小正数。
4、尺度变换和偏移:将xi乘以γ调整数值大小,再加上β增加偏移后得到yi,这里的γ是尺度因子,是β平移因子。
备注:这一步是Batch Normalization的精髓,由于归一化后的xi基本会被限制在正态分布下,使得网络的表达能力下降。为解决该问题,我们引入两个新的参数:γ,β。 γ和β是在训练时网络自己学习得到的。