PyTorch自动微分的详细介绍

1、PyTorch自动微分的入门例子

首先，我们先看一下PyTorch官网的入门例子，代码如下所示：

import torch

x = torch.ones(5)  # input tensor
y = torch.zeros(3)  # expected output
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

上述代码形成的动态图是这样的：

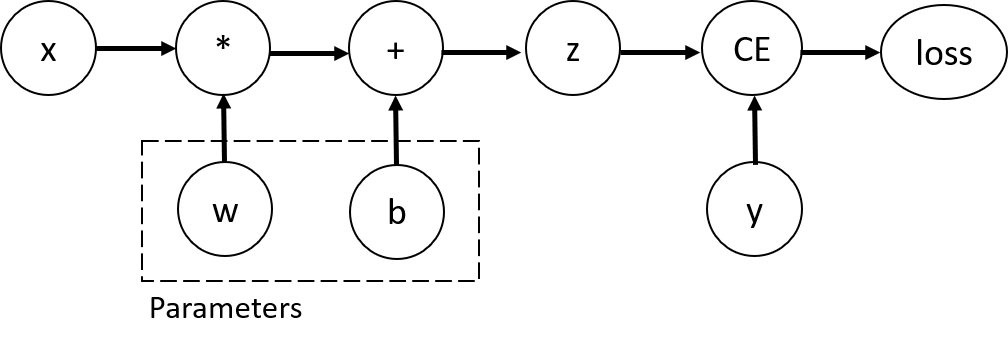
在这个网络中，w和b是我们需要优化的参数。因此，我们需要能够计算损失函数相对于这些变量的梯度。为了做到这一点，我们设置了这些张量的requires_grad属性。我们可以在创建张量时设置requires_grad的值，或稍后使用x.requires_grad_(True)方法设置。

为了计算梯度，我们需要调用loss.backward()，然后通过w.grad和b.grad获取到梯度值。

loss.backward()
print(w.grad)
print(b.grad)

结果如下所示：

tensor([[0.3313, 0.0626, 0.2530],
        [0.3313, 0.0626, 0.2530],
        [0.3313, 0.0626, 0.2530],
        [0.3313, 0.0626, 0.2530],
        [0.3313, 0.0626, 0.2530]])
tensor([0.3313, 0.0626, 0.2530])

2、PyTorch自动微分的进阶例子

上面的入门例子带领大家领略了自动微分的计算，得到了Tensor张量的梯度值，下面的例子带来大家学习一下如何通过梯度来更新向量。其重点是torch.no_grad()的代码，希望大家多读几遍。最后还要说明一下，这还是来源于PyTorch官网的例子。

import torch
import math

dtype = torch.float
device = "cuda" if torch.cuda.is_available() else "cpu"
torch.set_default_device(device)

# Create Tensors to hold input and outputs.
# By default, requires_grad=False, which indicates that we do not need to
# compute gradients with respect to these Tensors during the backward pass.
x = torch.linspace(-math.pi, math.pi, 2000, dtype=dtype)
y = torch.sin(x)

# Create random Tensors for weights. For a third order polynomial, we need
# 4 weights: y = a + b x + c x^2 + d x^3
# Setting requires_grad=True indicates that we want to compute gradients with
# respect to these Tensors during the backward pass.
a = torch.randn((), dtype=dtype, requires_grad=True)
b = torch.randn((), dtype=dtype, requires_grad=True)
c = torch.randn((), dtype=dtype, requires_grad=True)
d = torch.randn((), dtype=dtype, requires_grad=True)

learning_rate = 1e-6
for t in range(2000):
    # Forward pass: compute predicted y using operations on Tensors.
    y_pred = a + b * x + c * x ** 2 + d * x ** 3

    # Compute and print loss using operations on Tensors.
    # Now loss is a Tensor of shape (1,)
    # loss.item() gets the scalar value held in the loss.
    loss = (y_pred - y).pow(2).sum()
    if t % 100 == 99:
        print(t, loss.item())

    # Use autograd to compute the backward pass. This call will compute the
    # gradient of loss with respect to all Tensors with requires_grad=True.
    # After this call a.grad, b.grad. c.grad and d.grad will be Tensors holding
    # the gradient of the loss with respect to a, b, c, d respectively.
    loss.backward()

    # Manually update weights using gradient descent. Wrap in torch.no_grad()
    # because weights have requires_grad=True, but we don't need to track this
    # in autograd.
    with torch.no_grad():
        a -= learning_rate * a.grad
        b -= learning_rate * b.grad
        c -= learning_rate * c.grad
        d -= learning_rate * d.grad

        # Manually zero the gradients after updating weights
        a.grad = None
        b.grad = None
        c.grad = None
        d.grad = None

print(f'Result: y = {a.item()} + {b.item()} x + {c.item()} x^2 + {d.item()} x^3')

3、PyTorch自动微分中的计算图问题

当我们进行一次backward之后，各个节点的值会清除，这样进行第二次backward会报错，如果加上retain_graph==True后，可以再来一次backward。具体看下面的例子：

假设一个我们有一个输入x，y = x **2，z = y*4，然后我们有两个输出，一个output_1 = z.mean()，另一个output_2 = z.sum()，最后我们对两个output执行backward。

import torch
x = torch.randn((1,4),dtype=torch.float32,requires_grad=True)
y = x ** 2
z = y * 4
print(x)
print(y)
print(z)
loss1 = z.mean()
loss2 = z.sum()
print(loss1,loss2)
loss1.backward()    # 这个代码执行正常，但是执行完中间变量都释放了，所以下一个出现了问题
loss2.backward()    # 这时会引发错误

程序正常执行到最后一行报错：

RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time.

分析：计算节点数值保存了，但是计算图x-y-z结构被释放了，而计算loss2的backward仍然试图利用x-y-z的结构，因此会报错。

因此需要retain_graph参数为True去保留中间参数从而两个loss的backward()不会相互影响。正确的代码应当是：

# 假如你需要执行两次backward，先执行第一个的backward，再执行第二个backward
loss1.backward(retain_graph=True)# 这里参数表明保留backward后的中间参数。
loss2.backward() # 执行完这个后，所有中间变量都会被释放，以便下一次的循环

4、PyTorch backward()函数详解

PyTorch backward()函数原型是这样的：

torch.autograd.backward(tensors, grad_tensors=None, retain_graph=None, create_graph=False, grad_variables=None, inputs=None)

参考自：https://pytorch.org/docs/stable/generated/torch.autograd.backward.html

PyTorch在求导的过程中，分为下面两种情况：
（1）如果是标量对向量求导(scalar对tensor求导)，那么就可以保证上面的计算图的根节点只有一个，此时不用引入grad_tensors参数，直接调用backward函数即可。
（2）如果是向量对向量求导(tensor对tensor求导)，实际上是先求出Jacobian矩阵中每一个元素的梯度值(每一个元素的梯度值的求解过程对应上面的计算图的求解方法)，然后将这个Jacobian矩阵与grad_tensors参数对应的矩阵进行对应的点乘，得到最终的结果。

import torch
import torch.nn as nn

x = torch.tensor([2, 3, 4], dtype=torch.float, requires_grad=True)
print(x)
y = x * 2
while y.norm() < 1000:
    y = y * 2
print(y)

y.backward(torch.ones_like(y))
print(x.grad)

结果为：

tensor([2., 3., 4.], requires_grad=True)
tensor([ 512.,  768., 1024.], grad_fn=<MulBackward0>)
tensor([256., 256., 256.])

以前我们调用backward()函数时没有参数。这基本上相当于向后调用backward(torch.tensor(1.0))，这是一种在标量值函数的情况下计算梯度的有用方法，例如神经网络训练过程中的损失。

5、PyTorch 梯度累积

inp = torch.eye(4, 5, requires_grad=True)
out = (inp+1).pow(2).t()
out.backward(torch.ones_like(out), retain_graph=True)
print(f"First call\n{inp.grad}")
out.backward(torch.ones_like(out), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(out), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")

输出结果为：

First call
tensor([[4., 2., 2., 2., 2.],
        [2., 4., 2., 2., 2.],
        [2., 2., 4., 2., 2.],
        [2., 2., 2., 4., 2.]])

Second call
tensor([[8., 4., 4., 4., 4.],
        [4., 8., 4., 4., 4.],
        [4., 4., 8., 4., 4.],
        [4., 4., 4., 8., 4.]])

Call after zeroing gradients
tensor([[4., 2., 2., 2., 2.],
        [2., 4., 2., 2., 2.],
        [2., 2., 4., 2., 2.],
        [2., 2., 2., 4., 2.]])