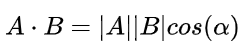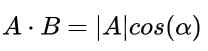备注:本文修改时间为2021年5月27日
大家好,我是飞燕网的站长,本文给大家说一下梯度以及梯度的物理意义吧。对于“梯度”这个东西,很多初学者搞不清楚,就连知乎上的大V,也是独乐乐不能与众乐乐,洋洋散散说了半天,读者也是一头雾水。
之所以大家对“梯度”一头雾水,这是因为大家没有一个明确的理解路线,站长对梯度的理解路线为:导数->偏导数->方向导数->方向->标量集合(最大值和最小值)->方向导数的数学定义变形记->内积的表示->梯度的表示形式->梯度和等高线……。本文希望通过这个系统化的学习路线,让大家能深刻地理解和掌握“梯度”这个机器学习和深度学习核心数学技术。再退一步来说,即便你读完了本文依然没有吃透梯度的含义,那么按照本文所倡导的“路线学习法”,也必能让自己对“梯度”的理解迈入一个新的台阶。
请大家集中精神,跟随站长的思路,你只要明白下面几点就行了:
(1)首先要明白什么是导数。导数反映的是函数沿坐标轴方向的变化率。这点大家应该都明白吧。
(2)接着要明白什么是偏导数。所谓偏导数,简单来说是对于一个多元函数,选定一个自变量并让其他自变量保持不变,只考察因变量与选定自变量的变化关系。数学上说,是指对于多元函数y=f(x1,x2,...xn),假设其偏导数都存在,则该函数共有n个偏导数,可以表示为:
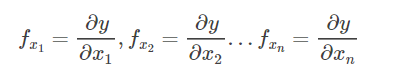
偏导数只能表示多元函数沿某个坐标轴方向的导数。
(3)接着要明白什么是方向导数。除了沿坐标轴方向上的导数,多元函数在非坐标轴方向上也可以求导数,这种导数称为方向导数。很容易发现,多元函数在特定点的方向导数有无穷多个,表示函数值在各个方向上的增长速度。
(4)上面说了方向导数,下面接着需要明白什么是方向。说到“方向”,估计很多读者此时一头雾水了,大家有方向感啊,出门都知道东南西北啊。no,我说的方向指的是坐标系中的方向,用角度表示,如下图所示:
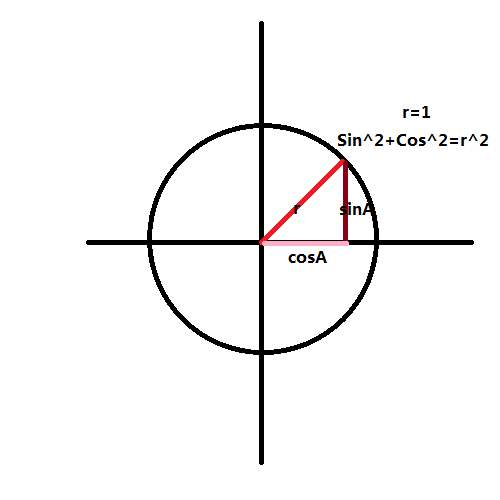
对于单位圆来说,sina和cosa函数的值分别表示与圆交点的纵坐标和横坐标。
(5)接着要深刻的认识方向导数是个标量,标量只有大小这一个属性;一个点有多个方向导数,这些方向导数必定存在最大值和最小值。
若有一个二元函数z=f(x, y),当它由点A移动到点B时(设移动的距离为L),此时函数值有一个增量M。当L趋于无限小时,若M/L有一个极限值,那么这个极限值就叫做函数在方向AB上的方向导数。
除了向B方向移动外,经过点A函数可以朝任意方向移动(当然移动的范围必须在定义域内),函数就有任意多个方向导数。因为方向导数属于标量,标量只有大小,所以这些方向导数里面肯定有最大和最小。
(6)上面一堆方向导数里面,只有一个方向上方向导数肯定最大。这个方向就用梯度(grad=ai+bj)这个向量来表示,其中a是函数在x方向上的偏导数,b是函数在y方向上的偏导数,梯度的模就是这个最大方向导数的值。
为什么说,一组方向导数的最大值对应的方向就是梯度呢?这是通过计算获得的。首先,我们来定义一下方向导数:

接着,我们对方向导数的定义进行变形:

引入单位向量之后,方向导数的定义变成了偏导数和单位向量的内积。关于内积的计算,如果大家不清楚,可以看看这个:
我们将内积表示为另一种我们熟悉的形式:
现在事情似乎是有点眉目了:A与B的内积等于A到B的投影长度乘以B的模。再进一步,如果我们假设B的模为1,即让|B|=1,那么就变成了:
也就是说,设向量B的模为1,则A与B的内积值等于A向B所在直线投影的矢量长度!这就是内积的一种几何解释,这个结论很重要。
(7)最后要明白梯度的表示形式。因为对方向导数的定义引入单位向量之后进行了变形,出现了偏导的集合,这个集合就是梯度,所以梯度的表示形式为:梯度是用倒三角来表示的,而且是用向量表示的,向量每个元素表示为偏导数
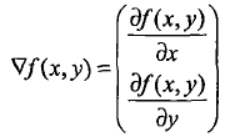
(8)梯度与等高线。略
(9)梯度下降法。略
......
关于梯度的内容其实有很多,但是即便写到此,站长相信大家只要认真的阅读本文一定能对梯度有深刻的理解。
后记:
上文是关于梯度的推导过程,关于偏导和梯度的更形象动画可以参考下面这个视频:
https://www.bilibili.com/video/BV1sW411775X

提醒:如果没有数学推导(见本文),站长认为仅仅看动画的效果并不好,顶多有点感性认识,过后仍然一头雾水。数学的魅力不在于动画展示,而在于推理过程和公式变形。
结束语
码字不易,欢迎大家关注飞燕网!