建好模型之后,必须对它进行评价,我们经常会使用一些评价指标来比较模型的预测准确度。常用的评价指标有:预测准确率,混淆矩阵,均方根误差等。
1、分类指标
1.1、预测准确率
简单的说,就是正确的预测所占的比例。虽然它很简单容易理解,但是我们无法通过它得知预测误差是如何产生的。
1.2、混淆矩阵
混淆矩阵可以进一步了解预测模型的优缺点。通过样本的采集,我们能够直接知道真实情况下,哪些数据结果是positive,哪些结果是negative。同时,我们通过用样本数据跑出分类型模型的结果,也可以知道模型认为这些数据哪些是positive,哪些是negative。因此,我们就能得到这样四个基础指标:
(1)真实值是positive,模型认为是positive的数量(True Positive=TP)
(2)真实值是positive,模型认为是negative的数量(False Negative=FN):这就是统计学上的第一类错误(Type I Error)
(3)真实值是negative,模型认为是positive的数量(False Positive=FP):这就是统计学上的第二类错误(Type II Error)
(4)真实值是negative,模型认为是negative的数量(True Negative=TN)
将这四个指标一起呈现在表格中,就能得到如下这样一个矩阵,我们称它为混淆矩阵(Confusion Matrix):
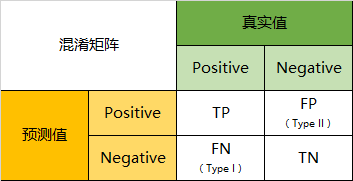
预测性分类模型,肯定是希望越准越好。那么,对应到混淆矩阵中,那肯定是希望TP与TN的数量大,而FP与FN的数量小。所以当我们得到了模型的混淆矩阵后,就需要去看有多少观测值在第二、四象限对应的位置,这里的数值越多越好;反之,在第一、三四象限对应位置出现的观测值肯定是越少越好。
但是,混淆矩阵里面统计的是个数,有时候面对大量的数据,光凭算个数,很难衡量模型的优劣。因此混淆矩阵在基本的统计结果上又延伸了如下4个指标:
(1)准确率(Accuracy):针对整个模型
(2)精确率(Precision)
(3)灵敏度(Sensitivity):就是召回率(Recall)
(4)特异度(Specificity)
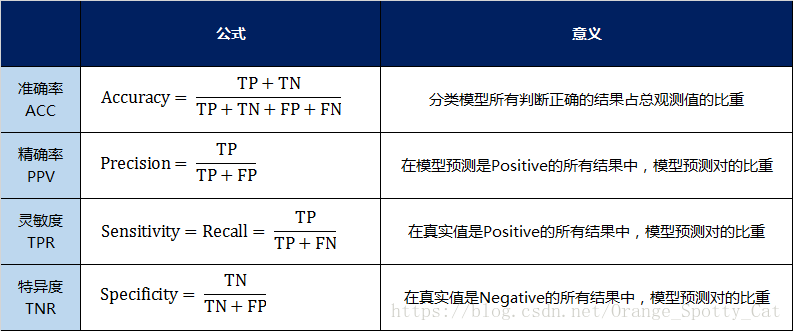
通过上面的四个指标,可以将混淆矩阵中数量的结果转化为0-1之间的比率。便于进行标准化的衡量。
1.3、对数损失指标
对二值变量和分类变量的预测通常以概率表示,比如顾客买鱼的概率。概率越接近100%,模型就越相信顾客会买鱼。对数损失指标利用这个置信度来校正其对预测误差的惩罚。具体来说,模型对错误预测的置信度越高,惩罚就越重。

在上图中,随着对错误预测的置信度接近最大值,惩罚程座鞋升。举例来说,如果模型预测顾客买鱼的概率为80%,但这最终证明息错的,那么就会被惩罚0.7分。然而,如果模型错误预测顾客买鱼的概率是99%,那么惩罚分数将高达2分。
随着模型对错误预测的置信度升高,惩罚也加重。由于对数损失指标根据对预测结果的置信度来调整惩罚程度,因此,它通常用于错误预测极其有害的情况。
2、回归指标
2.1、平均绝对误差
评价回归模型的一个简单方法是平等地惩罚所有预测误差,具体做法是对所有数据点的预测值和实际值之差取平均值。这个指标被称为平均绝对误差。
2.2、均方根误差
均方根误差是个常用的回归指标,尤其可用于避免较大的误差:因为每个误差都取了平方,所以大误差就被放大了。这使得均方根误差对异常值极其敏感,对这些值的惩罚力度也更大。
由于回归预测使用连续值,因此误差一般被量化成预测值和实际值之差,惩罚随误差大小而不同。
2.3、均方根对数误差
上面介绍了均方根误差这个指标,它可以加大对大误差的惩罚力度。除了考虑误差大小之外,还可以通过均方根对数误差把误差方向纳人考虑范围。以预测雨天顾客对雨伞的需求量为例,如果相比于高估,我们更希望避免低估,就可以使用这个指标。低估会引起顾客不满,进而造成收人损失,高估则只需增加库存。

